"The best solutions are often simple, yet unexpected."
-Julian Casablancas, The Strokes
Deep Learning (DL) has nearly taken over the machine learning world — in large part due to its great success in using layers of neural networks to discover the features in underlying data that actually matter to other, higher-level layers of neural networks.
When using Deep Learning to recognize a picture of a cat, for example, the lowest layers of the deep network learn to identify edges, light/dark gradients, etc. — visual features. Then higher levels learn how to combine those into patterns. And higher levels learn how patterns combine to make signature forms, and higher levels still learn to combine forms to recognize cats. (Why deep learning experts always use examples of cats will be the subject of another blog post.)
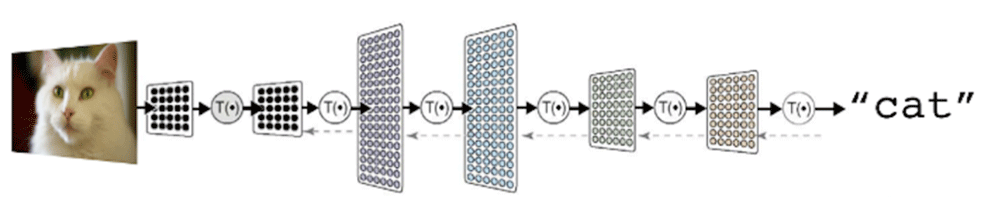
This has huge benefits in cases where the underlying features that matter most and in what combinations are just too complex to be discovered any other way. As a mathematician, I find Deep Learning networks a fascinating tool — nearly any reasonable transform can be learned given enough time and data.
Deep Learning can save the world from the hard problem of feature engineering. But is this always a good idea? It has significant disadvantages in constrained (embedded) environments.
Deep Learning is Very Inefficient
Deep Learning has ridiculously slow convergence compared to almost any other historical numerical method. Very smart mathematicians worked very hard over centuries to come up with optimal solutions to large classes of problems, like statistical inference from known distributions, approximation of many important types of functions, information analysis in linear algebra, and harmonic solutions like Fast Fourier Transforms. DL methods in effect cobble together unique, complicated constructs to solve each new problem – they may get to a similar place, but at cost of great inefficiency.
Take, for example, a simple, common problem in IoT: monitoring a piece of rotating equipment. A central tool in classic engineering in this area is the Fourier transform — vibrations and rotations have natural modes, i.e., frequencies, and monitoring power peaks and spectral shape reveals a lot of information. Some peaks are expected, while others are bad.
Stupid Deep Learning Tricks
Let's say we have a two-class problem where a Fast Fourier Transform (FFT) could neatly help distinguish between classes: Normal and Fault. (There are many problems where a simple FFT would not be sufficient, but there are also a great many where they work quite well.)
But instead of running an FFT and using those features as model input, let's say we construct a Deep Learning model and ask it to learn our two classes — in effect hoping to replicate this Fourier Transform in the lower levels of the deep network.
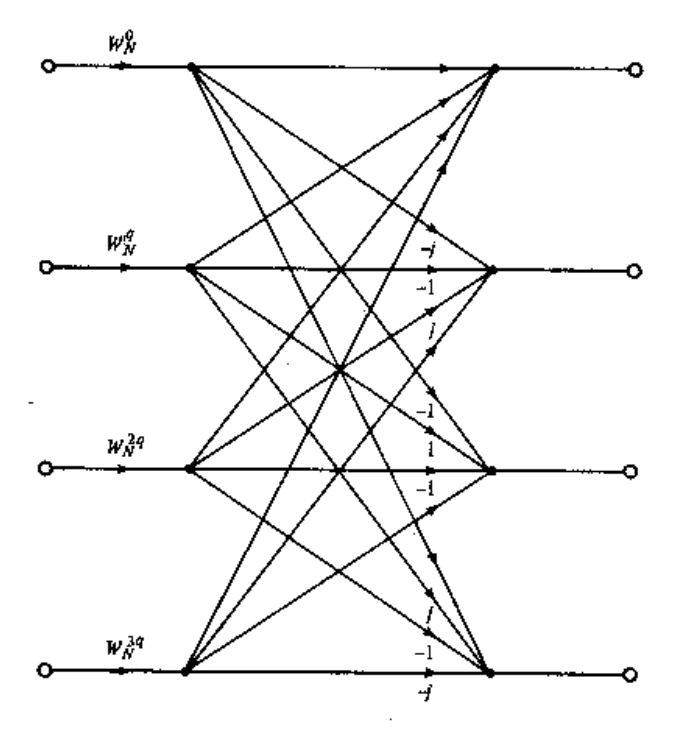
The FFT is a brilliant, human-designed algorithm to achieve what is called a Discrete Fourier Transform (DFT). But the DFT is basically a linear matrix operation, so it's fairly simple to map the DFT to a neural network. It's going to look like a single layer, fully connected set of nodes, with (ideally) weights near the DFT matrix, and a linear activation function. Here's an example of someone who tried it on GitHub.
This single feature layer could then connect to higher layers to make decisions based on Fourier peaks. But consider the pieces here:
- In order to get this simple representation, we actually had to use a linear activation function for this layer. In practice, one tends to build homogeneous networks with nonlinear activation functions at all stages. So to converge on a DFT will actually require much more machinery if the practitioner takes a more standard DL approach.
- To get this to converge close to an actual DFT requires a large, well-organized set of example data that spans the frequency spaces. Actual data from the actual vibrating or rotating device is probably not going to provide that kind of diversity, creating a real network training problem that may not be possible to overcome.
- Even this "best case" network representation of a DFT, requires O(n²) multiplies. The whole brilliance of the FFT is that it requires O(n log(n)). Why would you deliberately nearly square the number of operations you are going to put on an embedded chip!?!
The FFT is only one of many examples of feature space operations that needlessly bog down when learned by neural networks. There are even more efficient ways to mathematically represent the "important frequency peak" IoT problem we described, but which would be effectively impossible for DL networks to model without vast computational resources.
"The FFT is only one of many examples of feature space operations that needlessly bog down when learned by neural networks."
There are even simpler transforms that neural networks struggle with. Something as basic as a square or a square root operation requires hidden layer networks and a disproportionately large number of nodes to solve accurately. Obvious engineering measures like a standard deviation or RMS energy, are terribly inefficient to learn and compute.
Feature Engineering is a Better Way, Especially for Embedded and Constrained Use Cases
Learning mathematical features from scratch is possible with DL. But it may be a bad idea for some problems, and it is certainly a losing game for constrained or embedded applications where every clock cycle and byte of memory counts. Using DL for feature discovery is a huge waste of resources if a more direct route is available. Far better for these applications is to focus on engineering solid features that are known or can be shown to separate and distinguish between target classes.
Our approach is grounded in automated, smart feature engineering. We use a machine learning guided process to explore a huge variety of well-understood mathematical and engineering feature spaces and to apply mechanisms such as sparse-coding to converge on features much faster and express them more efficiently than can be done with DL.
This has two advantages:
- The resulting feature computations are computationally efficient and can be put on any architecture – including constrained or embedded environments.
- The results are explainable in terms of underlying physics and time-frequency behaviors — no black boxes required.
Machine learning with feature spaces discovered in this way can still leverage the strengths of machine learning for making rich decisions, but they enable simpler algorithms, like SVMs, decision trees or smaller neural networks, to be deployed, leading to huge savings vs. Deep Learning.
Deep learning has been used to achieve some remarkable things in recent years. But it's not the solution to every problem. To paraphrase Robert Heinlein, for some problems, it's a bit like trying to teach a pig to sing. It wastes your time, and it annoys the pig.
