レーダートランシーバー：ＡＤＡＳ／自動運転のキーコンポーネント
- Blog 1: レーダーはなぜ必要か？
- Blog 2: FMCWレーダーの基本
- Blog 3: 距離測定：レーダーはどこまで検知できるか？
- Blog 4: レーダーの解像度：レーダーはどの程度の精度が出せるのか？
- Blog 5: レーダーアーキテクチャ：複数のレーダーセンサーを接続する
車載用レーダーを紹介するシリーズの前回のブログでは、検知距離に影響するレーダートランシーバーのパラメータを分析しました。ここでは、検知精度を上げる方法について、視野角、距離分解能、角度分解能に着目して説明します。確かなことは、できるだけ遠くを“見通す”だけでは十分ではなく、距離においても角度（方位）においても近接した２つのターゲットを区別できることも重要です。
距離分解能
レーダーが定義する距離分解能とは、同じ角度方向（方位）に置かれた、レーダーからの距離が異なるターゲットを区別できる能力です。図1は2つのターゲットで反射した信号を時間領域で表したもので、図2はFFT（高速フーリエ変換）後の各ターゲットに対応するベースバンド周波数（周波数シフト）を示しています。
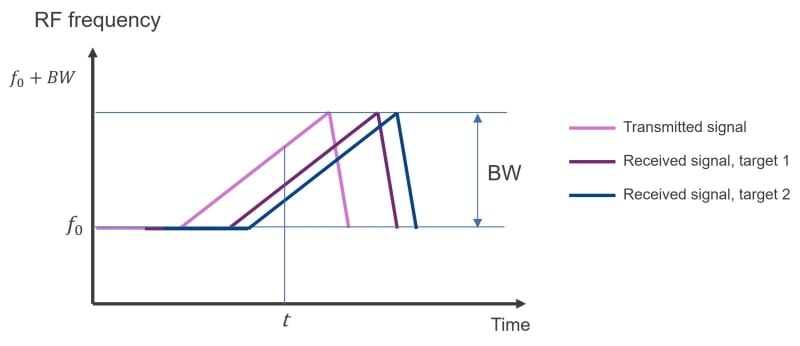
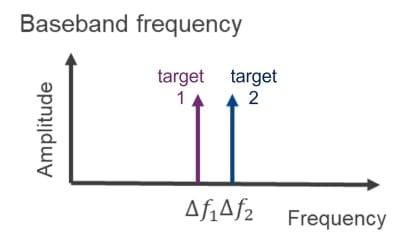
2つのターゲットが近いほど、ベースバンド周波数 ∆f1 と ∆f2の差は小さくなります。ある間隔まで近づくとレーダーシステムは2つのターゲットを分離できなくなります。この最小周波数シフトつまり最小間隔が1つのFFTビン(FFT bin)に相当します。ターゲットを分離可能な周波数の差∆fは計測時間 Tcで割ることで求めることができます。
∆fは計測時間を長くすることで改善、すなわち最小化することができます。ターゲット間距離∆Rと∆fは直接関係しています。cは光速です。
ここで、Sは送信レーダー信号の傾き（チャープレート：Hz/s ）です。帯域幅は、信号の傾きと持続時間の積であるため、距離分解能dresは信号帯域幅の関数として表すことができます。
表1に示すように、レーダーチャープの帯域幅は距離分解能に直接影響します。
表 1: 距離分解能 vs. レーダーチャープ帯域幅
| Bandwidth | Range resolution dres |
|---|---|
| 250 MHz | 60 cm |
| 500 MHz | 30 cm |
| 1 GHz | 15 cm |
| 2 GHz | 7.5 cm |
| 4 GHz | 3.75 cm |
イメージングレーダーなど、高い解像度が必要なアプリケーションでは、広い帯域が必要です。しかし、長距離レーダーのようなアプリケーションでは、センチメートル単位の精度は必要ないため、より狭い帯域幅で十分です。レーダーの最大到達距離は帯域幅に反比例するため、この点を考慮することも重要です。
あるサンプリングレートFsにおいて、帯域を広げることは検知距離を短くすることになります。
視野角(FOV: Field of View)
ターゲットの方向（方位）を明確に特定することも重要です。図3と図4に示すように、方位の特定はレーダーの視野角の範囲内においてのみ可能で、方位角と仰角でレーダーの角度範囲を定めています。
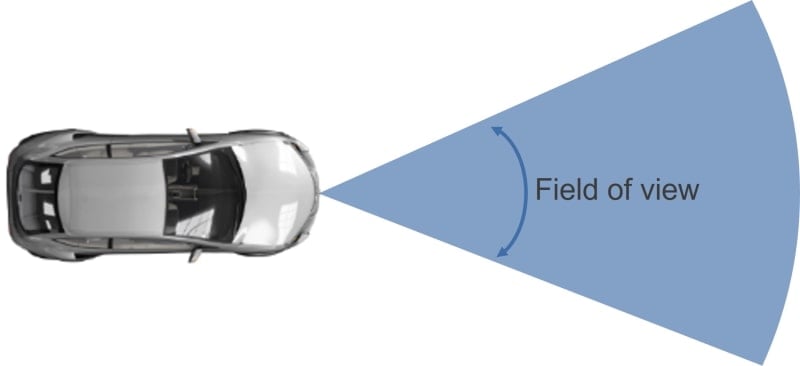
車載レーダーは、反射波の到来角（AoA: Angle of Arrival）を特定するため、つまり、障害物の角度位置を特定するために複数の受信アンテナを使用します。そのため、アンテナアレイの形状は視野角の決定要因となります。
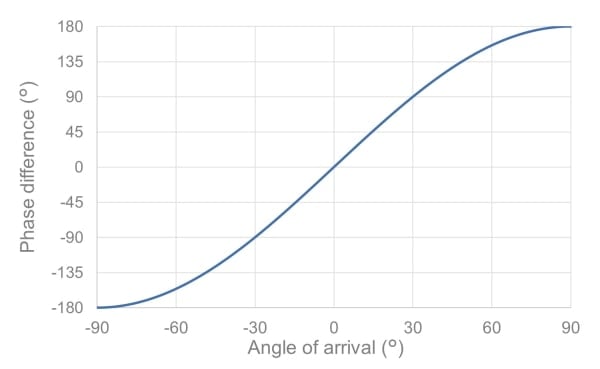
送信アンテナが1つの場合、視野角は受信アンテナの形状と放射特性によって決まります。ここで、距離dだけ離れた2つの受信アンテナについて考えてみましょう。信号の到来角は、それぞれのアンテナで受信した信号の位相差を比較することで計算することができます。受信信号の位相差は、図5に示すように、周波数（波長）とアンテナ間の距離に依存します。
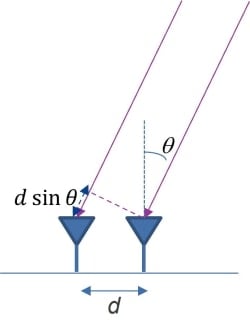
到来角を明確に測定できる角度範囲は、位相差が単調に変化する-180°から+180°までの範囲であるので、単に幾何学的な観点で、理論上の視野角は次式で与えられまる。
最大視野角は-90°から+90°までのすべての到来角を検出できるときであり、これは、図6に示すように、アンテナ間の距離が動作周波数における波長の半分、すなわち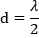
に等しい場合です。
77GHzの車載レーダーの場合、アンテナ間隔を約2mmにすることで理論上の視野を最大にすることができます。これは、使用するアンテナが等方性放射体であると仮定した場合です。現実には、アンテナの放射パターンによって、視野はさらに制限されます。
ここで、図7に示すように、受信アンテナは2つの均一な直線状のパッチアレイであると考えます。
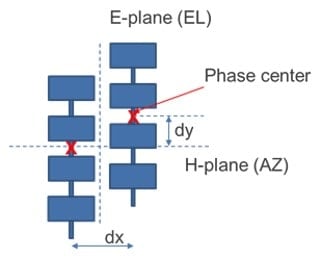
この場合、方位方向のアンテナパターンは非常に広く（パッチアンテナに相当）、視野角に与える影響は限定的です。アンテナ列の間隔dxが主に影響し、視野角は式(6)を用いて計算することができます。
仰角方向の視野角については、垂直方向の列のすべてのパッチアンテナを1つのアンテナと見なします。理論的な視野角を計算するためには、列の位相中心（つまり、アンテナ縦列からの放射の総和が発生すると想定した点）を考慮する必要があります。仰角方向の理論的な視野角は、各縦列の位相中心間の垂直方向の間隔（dy）によって制限されることになります。この距離が半波長であれば、原理的に最大の視野を得ることができます。しかし、このアンテナの場合はアンテナビームの半値幅（HPBW: Half Power BeamWidth ）が小さくなるので（〜20〜25°）、アンテナビームより広角では検出できません。このように、放射パターンが視野の制限要因となります。
角度分解能
距離分解能の場合と同様に、同じ距離で異なる角度（方位）に置かれた2つの異なるターゲットを区別できることも重要です。この場合は、それぞれのターゲットからの信号遅延による周波数シフトを用いてターゲットを識別することはできません。ここでも異なる位置の複数アンテナによるダイバーシティが必要となります。
角度分解能θresはレーダーで区別できる最小の角度間隔を示します。送信アンテナが1つの場合、次のように計算できます。
Nは受信アンテナ数、θは到来角です。角度分解能はボアサイト付近の方位(θ = 0°)で最大となります。
視野角を最大化するためにアンテナ間隔を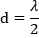とすると、角度分解能は周波数によらず、受信アンテナの数のみで決まります。
したがって、アンテナの本数を増やすことで角度分解能を上げることができます。これは、レーダーMMICトランシーバーのチャンネル数を増やすことで可能となります。さらに、複数の送信アンテナを使用したMIMO（Multiple Input, Multiple Output）や高解像のデータ処理を行うことで、分解能をさらに向上させることができます。
Conclusion
今回は、レーダーシステムの精度を決定するパラメータを紹介しました。距離分解能はレーダートランシーバーの性能が直接影響し、角度分解能と視野はレーダーシステムで使用するアンテナ形状に依存します。
次回のブログでは、現在および将来のアプリケーションに必要な様々なレーダーアーキテクチャに焦点を当てます。